
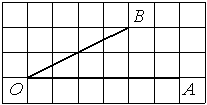
 Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
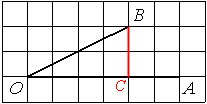 В данной задаче надо просто дорисовать угол до прямоугольного треугольника. При этом длину сторон угла можно выбрать по своему усмотрению, поэтому выберем так, чтобы стороны составляли целое число клеточек.
В данной задаче надо просто дорисовать угол до прямоугольного треугольника. При этом длину сторон угла можно выбрать по своему усмотрению, поэтому выберем так, чтобы стороны составляли целое число клеточек.
Тогда по определению тангенса:
tg∠BOC=BC/OC=2/4=0,5
Ответ: 0,5
Поделитесь решением
Присоединяйтесь к нам...
 Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, описанной около этого треугольника.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, описанной около этого треугольника.
Стороны AC, AB, BC треугольника ABC равны 2√
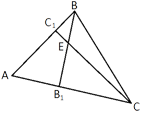 Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
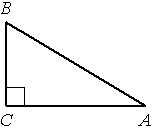 В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.





Комментарии: