
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ734 –ł–∑ 1087 |
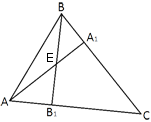 –í—č—Ā–ĺ—ā—č AA1 –ł BB1 –ĺ—Ā—ā—Ä–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ E. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —É–≥–Ľ—č AA1B1 –ł ABB1 —Ä–į–≤–Ĺ—č.
–í—č—Ā–ĺ—ā—č AA1 –ł BB1 –ĺ—Ā—ā—Ä–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ E. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —É–≥–Ľ—č AA1B1 –ł ABB1 —Ä–į–≤–Ĺ—č.
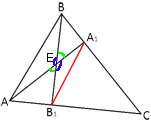 –ü—Ä–ĺ–≤–Ķ–ī–Ķ–ľ –ĺ—ā—Ä–Ķ–∑–ĺ–ļ A1B1 –ł —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł EB1A –ł EA1B.
–ü—Ä–ĺ–≤–Ķ–ī–Ķ–ľ –ĺ—ā—Ä–Ķ–∑–ĺ–ļ A1B1 –ł —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł EB1A –ł EA1B.
∠A1EB=∠B1EA (—ā–į–ļ –ļ–į–ļ –ĺ–Ĺ–ł
–≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ—č–Ķ).
∠EB1A=∠EA1B=90¬į (—ā–į–ļ –ļ–į–ļ BB1 –ł AA1 -
–≤—č—Ā–ĺ—ā—č).
–ü–ĺ
–Ņ–Ķ—Ä–≤–ĺ–ľ—É –Ņ—Ä–ł–∑–Ĺ–į–ļ—É –Ņ–ĺ–ī–ĺ–Ī–ł—Ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤, —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ–ľ—č–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł
–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ:
EB1/EA1=EA/EB
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł EA1B1 –ł EAB
∠BEA=∠B1EA1 (—ā–į–ļ –ļ–į–ļ –ĺ–Ĺ–ł
–≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ—č–Ķ).
–ö–į–ļ –ľ—č –≤—č—Ź—Ā–Ĺ–ł–Ľ–ł —Ä–į–Ĺ–Ķ–Ķ:
EB1/EA1=EA/EB
–£–ľ–Ĺ–ĺ–∂–ł–ľ –Ľ–Ķ–≤—É—é –ł –Ņ—Ä–į–≤—É—é —á–į—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į –Ĺ–į EA1, –Ņ–ĺ–Ľ—É—á–ł–ľ:
EB1=EA1*EA/EB
–†–į–∑–ī–Ķ–Ľ–ł–ľ –Ľ–Ķ–≤—É—é –ł –Ņ—Ä–į–≤—É—é —á–į—Ā—ā–ł –Ĺ–į EA, –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ:
EB1/EA=EA1/EB
–ü–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź, —á—ā–ĺ –Ņ–ĺ
–≤—ā–ĺ—Ä–ĺ–ľ—É –Ņ—Ä–ł–∑–Ĺ–į–ļ—É –Ņ–ĺ–ī–ĺ–Ī–ł—Ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤, —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł EA1B1 –ł EAB
–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –Ņ–ĺ
–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é, —É–≥–Ľ—č AA1B1 –ł ABB1 —Ä–į–≤–Ĺ—č.
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –°—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–ĺ–ľ–Ī–į —Ä–į–≤–Ĺ–į 9, –į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —Ü–Ķ–Ĺ—ā—Ä–į —Ä–ĺ–ľ–Ī–į –ī–ĺ –Ĺ–Ķ—Ď —Ä–į–≤–Ĺ–ĺ 1. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —Ä–ĺ–ľ–Ī–į.
–°—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–ĺ–ľ–Ī–į —Ä–į–≤–Ĺ–į 9, –į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —Ü–Ķ–Ĺ—ā—Ä–į —Ä–ĺ–ľ–Ī–į –ī–ĺ –Ĺ–Ķ—Ď —Ä–į–≤–Ĺ–ĺ 1. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —Ä–ĺ–ľ–Ī–į.
 –Ď–ĺ–ļ–ĺ–≤–į—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 10, –į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ —Ä–į–≤–Ĺ–ĺ 12. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ć—ā–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į.
–Ď–ĺ–ļ–ĺ–≤–į—Ź —Ā—ā–ĺ—Ä–ĺ–Ĺ–į —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 10, –į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ —Ä–į–≤–Ĺ–ĺ 12. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ć—ā–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į.
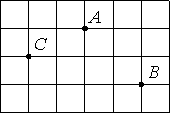 –Ě–į –ļ–Ľ–Ķ—ā—á–į—ā–ĺ–Ļ –Ī—É–ľ–į–≥–Ķ –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ—č —ā–ĺ—á–ļ–ł A, B –ł C. –ü–Ľ–ĺ—Č–į–ī—Ć –ĺ–ī–Ĺ–ĺ–Ļ –ļ–Ľ–Ķ—ā–ļ–ł —Ä–į–≤–Ĺ–į 1. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł A –ī–ĺ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č –ĺ—ā—Ä–Ķ–∑–ļ–į BC.
–Ě–į –ļ–Ľ–Ķ—ā—á–į—ā–ĺ–Ļ –Ī—É–ľ–į–≥–Ķ –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ—č —ā–ĺ—á–ļ–ł A, B –ł C. –ü–Ľ–ĺ—Č–į–ī—Ć –ĺ–ī–Ĺ–ĺ–Ļ –ļ–Ľ–Ķ—ā–ļ–ł —Ä–į–≤–Ĺ–į 1. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł A –ī–ĺ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č –ĺ—ā—Ä–Ķ–∑–ļ–į BC.
 –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ AC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ –≤–Ķ—Ä—ą–ł–Ĺ—É C –ł –ļ–į—Ā–į–Ķ—ā—Ā—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ AB –≤ —ā–ĺ—á–ļ–Ķ B. –Ě–į–Ļ–ī–ł—ā–Ķ AC, –Ķ—Ā–Ľ–ł –ī–ł–į–ľ–Ķ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ 7.5, –į AB=2.
–ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ AC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ –≤–Ķ—Ä—ą–ł–Ĺ—É C –ł –ļ–į—Ā–į–Ķ—ā—Ā—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ AB –≤ —ā–ĺ—á–ļ–Ķ B. –Ě–į–Ļ–ī–ł—ā–Ķ AC, –Ķ—Ā–Ľ–ł –ī–ł–į–ľ–Ķ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ 7.5, –į AB=2.
 –í –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ –ě –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ—č –ī–ł–į–ľ–Ķ—ā—Ä—č AD –ł BC, —É–≥–ĺ–Ľ ABO —Ä–į–≤–Ķ–Ĺ 75¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į ODC.
–í –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ –ě –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ—č –ī–ł–į–ľ–Ķ—ā—Ä—č AD –ł BC, —É–≥–ĺ–Ľ ABO —Ä–į–≤–Ķ–Ĺ 75¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į ODC.



–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł:
(2017-05-10 22:22:34) –ź–ī–ľ–ł–Ĺ–ł—Ā—ā—Ä–į—ā–ĺ—Ä: –Ē–ľ–ł—ā—Ä–ł–Ļ, –Ķ—Ā–Ľ–ł –Ĺ–Ķ —Ā–Ľ–ĺ–∂–Ĺ–ĺ, —ā–ĺ –Ņ—Ä–ł—ą–Ľ–ł—ā–Ķ, –Ņ–ĺ–∂–į–Ľ—É–Ļ—Ā—ā–į, –í–į—ą –≤–į—Ä–ł–į–Ĺ—ā —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –Ĺ–į admin@otvet-gotov.ru
(2017-05-08 09:36:21) –Ē–ľ–ł—ā—Ä–ł–Ļ: –° –Ņ–ĺ–ľ–ĺ—Č—Ć—é –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –ļ–ĺ—Ä–ĺ—á–Ķ –ł –Ľ–Ķ–≥—á–Ķ