В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
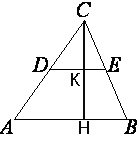Проведем
высоту CH.
Средняя линия делит CH пополам, как и стороны треугольника.
Следовательно, CK=KH.
По
теореме о средней линии AB=2DE.
SCDE=DE*CK/2=35.
DE*CK=70
SABC=AB*CH/2=2DE*2CK/2=2DE*CK=2*70=140
Ответ: SABC=140
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 968√
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Медиана равностороннего треугольника равна 9√
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: