Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
Пусть:
∠KMP=44°
∠MKP=71°
∠KPM=65°
Рассмотрим треугольник AMK.
AM=AK (по
второму свойству касательной)
Следовательно треугольник AMK -
равнобедренный, тогда, по
свойству равнобедренного треугольника:
∠AMK=∠AKM
Заметим, что оба этих угла охватывают дугу MK, и следовательно равны половине ее градусной меры (по
свойству углов на окружности).
∠KPM является
вписанным в окружность углом и опирается на эту же дугу, следовательно и он равен половине градусной меры этой дуги.
Получается, что:
∠AMK=∠AKM=∠KPM=65°
Применив
теорему о сумме углов треугольника:
180°=∠AMK+∠AKM+∠MAK
180°=65°+65°+∠MAK
∠MAK=50°
Аналогично, для двух других треугольников получим:
∠BKP=∠BPK=∠KMP=44°
∠KBP=180°-44°-44°=92°
И...
∠CPM=∠CMP=∠MKP=71°
∠PCM=180°-71°-71°=38°
Ответ: 50°, 92° и 38°
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AMB.
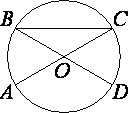В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Точка О – центр окружности, /ACB=25° (см. рисунок). Найдите величину угла AOB (в градусах).
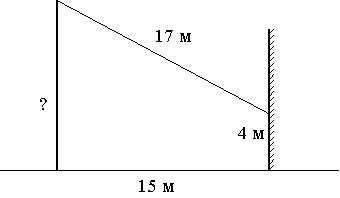От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
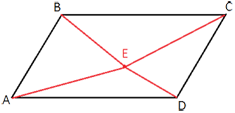Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: