В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
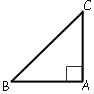SABC=AB*AC/2
Пусть угол, равный 45° будет угол В.
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=90°+45°+∠C
∠C=45°
Следовательно, по
свойству равнобедренного треугольника, треугольник ABC -
равнобедренный.
Значит AB=AC.
По
теореме Пифагора:
BC2=AB2+AC2
BC2=AB2+AB2
822=2AB2
6724=2AB2
AB2=3362
SABC=AB*AC/2
SABC=AB2/2=3362/2=1681
Ответ: SABC=1681
Поделитесь решением
Присоединяйтесь к нам...
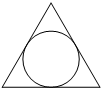Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
Лестница соединяет точки A и B. Высота каждой ступени равна 13 см, а длина – 84 см. Расстояние между точками A и B составляет 25,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 8 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. Найдите длину троса.
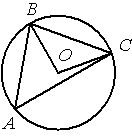Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: