
 На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
Вариант 1 Предложил Андрей Середников
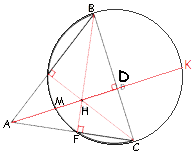 Дорисуем полуокружность до полной окружности.
Дорисуем полуокружность до полной окружности.
Продлим
высоту AD до пересечения с окружностью, обозначим точку пересечения К.
Обозначим F как точку пересечения окружности и стороны AC.
BF - является
высотой треугольника ABC, так как для окружности ∠BFC -
вписанный угол, который опирается на дугу в 180° (BC - диаметр), следовательно ∠BFC=180°/2=90°
1) AF*AC=AM*AK (по
теореме о двух секущих).
2) Рассмотрим
хорду MK.
BC - перпендикуляр к MK, проходящий через центр окружности, следовательно BC -
серединный перпендикуляр.
Это значит, BC делит
хорду MK пополам, т.е. MD=KD=18
3) Рассмотрим треугольники AHF и ACD.
∠DAC - общий.
∠AFH=∠ADC - это прямые углы.
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, по определению
подобия, мы можем записать:
AC/AH=AD/AF => AC*AF=AD*AH
В п. 1) мы получили равенство AF*AC=AM*AK, тогда:
AM*AK=AD*AH
AH=AM*AK/AD
Из рисунка находим:
AM=AD-MD=27-18=9
AK=AD+KD=27+18=45
Тогда:
AH=9*45/27=45/3=15
Ответ: AH=15
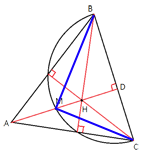 Проведем отрезки CM и MB.
Проведем отрезки CM и MB.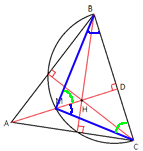 Рассмотрим треугольники MBC и MDС.
Рассмотрим треугольники MBC и MDС.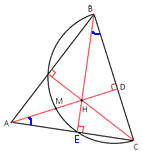 Вернемся к первоначальному рисунку и рассмотрим треугольники AHE и BHD.
Вернемся к первоначальному рисунку и рассмотрим треугольники AHE и BHD.Поделитесь решением
Присоединяйтесь к нам...
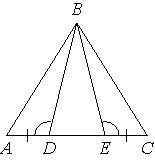 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
 Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=40.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=40.
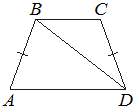 В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
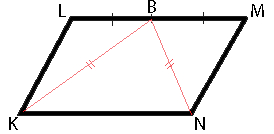 В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.
Комментарии:
(2016-12-08 19:09:59) Администратор: Юлия, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-12-08 15:19:31) Юлия : На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки АМ и АК. Докажите что треугольник ВСМ=треугольникуСВК.
(2015-02-14 16:05:23) Денис: Могу скинуть решение: ppepsicola@mail.ru (захожу не каждый день)
(2015-02-14 16:04:36) Денис:: решал немного по-другому, получилось 22,5