На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
Рассмотрим треугольник АВЕ.
/B=90° (т.к. ABCD -
прямоугольник).
/EAB=45° (по условию задачи).
Тогда по
теореме о сумме углов треугольника /BEA=180°-/B-/EAB=180°-90°-45°=45°.
Следовательно, треугольник ABE -
равнобедренный (по
свойству). Тогда AB=BE (по
определению равнобедренного треугольника).
EC=BC-BE=17-12=5 (т.к. BC=AD).
Рассмотрим треугольник ECD.
Он
прямоугольный (т.к. угол С - прямой).
Тогда по
теореме Пифагора получаем:
ED2=CD2+EC2
ED2=122+52
ED2=144+25=169
ED=13
Ответ: ED=13
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 128√
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна
180°, то эти прямые параллельны.
3) Площадь треугольника не превышает произведения двух его сторон.
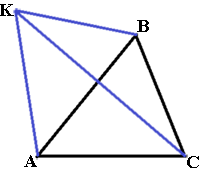Стороны AC, AB, BC треугольника ABC равны 2√
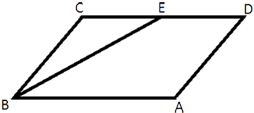Площадь параллелограмма
ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: