
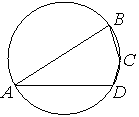 Угол A четырёхугольника ABCD, вписанного в окружность, равен 33°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Угол A четырёхугольника ABCD, вписанного в окружность, равен 33°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Так как четырехугольник вписан в окружность, то по свойству описанной окружности:
∠A+∠C=180°
∠C=180°-∠A=180°-33°=147°
Ответ: 147
Поделитесь решением
Присоединяйтесь к нам...
 Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
Стороны AC, AB, BC треугольника ABC равны 2√
 В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
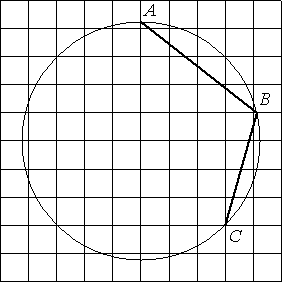 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
Комментарии: