Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=44, MN=24. Площадь треугольника ABC равна 121. Найдите площадь треугольника MBN.
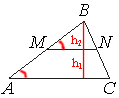Рассмотрим треугольники ABC и MBN.
∠ABC - общий.
∠BAC=∠BMN
Следовательно, по первому признаку подобия, эти треугольники подобны.
Площади треугольника ABC:
SABC=(1/2)AC*h1
121=(1/2)*44*h1
h1=121*2/44=121/22=5,5
Из подобия треугольников получаем пропорцию:
AC/MN=h1/h2
h2=MN*h1/AC=24*5,5/44=24/8=3
Тогда площадь треугольника MBN:
SMBN=(1/2)MN*h2
SMBN=(1/2)*24*3=12*3=36
Ответ: 36
Поделитесь решением
Присоединяйтесь к нам...
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
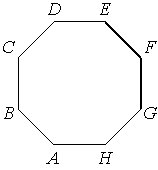ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
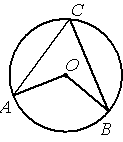Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 57.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: