
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
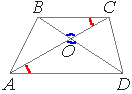 Рассмотрим треугольники AOD и BOC.
Рассмотрим треугольники AOD и BOC.
По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда:
∠DAO=∠BCO (накрест лежащие углы).
∠AOD=∠BOC (вертикальные углы).
Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Следовательно, можем записать пропорцию:
AD/BC=AO/OC
7/3=AO/OC
7*OC=3*AO
При этом AO+OC=AC=20
OC=20-AO, подставляем это равенство в ранее полученную пропорцию:
7*(20-AO)=3*AO
140-7*AO=3*AO
140=7*AO+3*AO
140=10*AO
AO=140/10=14
Ответ: 14
Поделитесь решением
Присоединяйтесь к нам...
 Человек ростом 1,5 м стоит на расстоянии 7 м от столба, на котором висит фонарь на высоте 3,6 м. Найдите длину тени человека в метрах.
Человек ростом 1,5 м стоит на расстоянии 7 м от столба, на котором висит фонарь на высоте 3,6 м. Найдите длину тени человека в метрах.
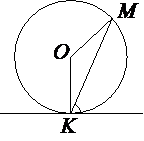 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
 В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=1°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=1°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Комментарии:
(2024-01-23 18:12:02) Али: В трапеции � � � � ABCDс основаниями � � = 4 BC=4и � � = 1 6 AD=16диагонали пересекаются в точке � . O.Найдите � � , OC,если � � = 1 2 . AC=12.