
 Проектор полностью освещает экран A высотой 190 см, расположенный
на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
Проектор полностью освещает экран A высотой 190 см, расположенный
на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
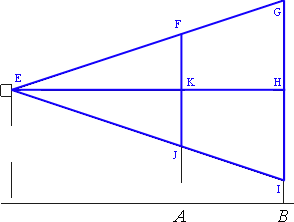 Обозначим треугольники и их ключевые точки как показано на рисунке.
Обозначим треугольники и их ключевые точки как показано на рисунке.
Рассмотрим треугольники EGI и EFJ.
Прямая EH перпендикулярна обоим экранам и проходит через их центр, следовательно является
серединным перпендикуляром.
То есть:
FK=FJ/2=190/2=95
GH=GI/2=380/2=190
Рассмотрим треугольники EFK и EGH.
∠FEK - общий для обоих треугольников.
∠EKF=∠EHG=90° (т.к. EH -
серединный перпендикуляр).
Тогда, по
первому признаку подобия, данные треугольники
подобны.
Следовательно, мы можем записать пропорцию сторон:
EH/EK=GH/FK
EH/210=190/95
EH=(210*190)/95=210*2=420
Ответ: 420
Поделитесь решением
Присоединяйтесь к нам...
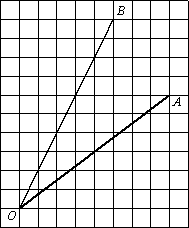 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
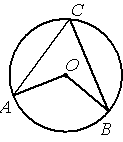 Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
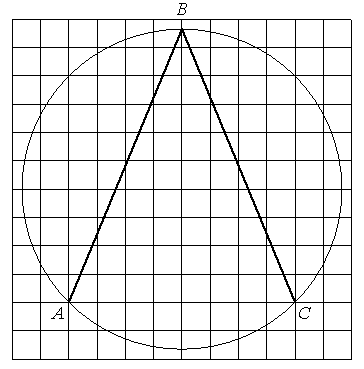 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
 ABCDEFGHI – правильный девятиугольник. Найдите угол BAG. Ответ дайте в градусах.
ABCDEFGHI – правильный девятиугольник. Найдите угол BAG. Ответ дайте в градусах.
 Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Комментарии: