
 Периметр треугольника равен 48, одна из сторон равна 18,
а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
Периметр треугольника равен 48, одна из сторон равна 18,
а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
По третьему свойству вписанной окружности, радиус вписанной окружности равен:
r=S/p, где S - площадь треугольника, а p - полупериметр.
p=48/2=24
S=r*p=3*24=72
Ответ: 72
Поделитесь решением
Присоединяйтесь к нам...
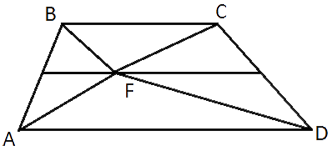 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
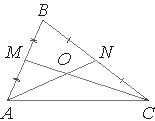 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
 В треугольнике ABC AB=BC=53, AC=56. Найдите длину медианы BM.
В треугольнике ABC AB=BC=53, AC=56. Найдите длину медианы BM.
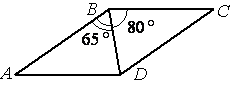 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
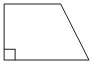 Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Комментарии:
(2023-04-26 20:11:27) галина: есть ли другое решение задачи 936 из1087 для чего дается сторона
(2023-04-26 20:03:19) галина: все свойства вписанной окружности