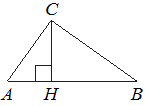
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
Рассмотрим треугольники ACH и BCH.
Докажем, что это подобные треугольники:
∠AHC=∠BHC=90° (так как CH -
высота).
По
теореме о сумме углов треугольника:
180°=∠CAH+∠AHC+∠HCA
180°=∠CAH+90°+∠HCA
90°=∠CAH+∠HCA
∠CAH=90°-∠HCA
Заметим, что:
∠BCH=90°-∠HCA
Получается, что ∠CAH=∠BCH
Тогда, по первому признаку подобия, данные треугольники подобны, т.е. можем записать пропорцию:
AH/CH=CH/BH
AH*BH=CH2
2*18=CH2
36=CH2
CH=√36=6
Ответ: 6
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь трапеции, изображённой на рисунке.
Найдите угол ABC . Ответ дайте в градусах.
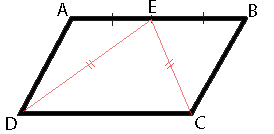В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
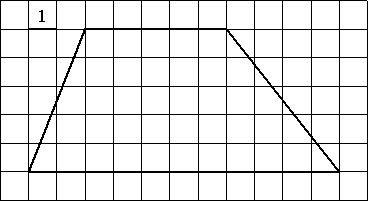Найдите площадь трапеции, изображённой на рисунке.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=4:1.Прямая AK пересекает сторону BC в точке P.Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2024-02-28 13:41:15) Юля: Прямая параллельная стороне АС треугольника АВС , пересекает стороны АВ и ВС в точках М и N соответственно. АВ =8 , АС =8 , МN= 2 Найдите АМ