Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=40.
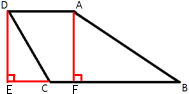Дочертим отрезки как показано на рисунке.
DE=AF, т.к. это
высоты
трапеции.
∠DCE=180°-∠BCD=180°-120°=60° (т.к. это
смежные углы).
sin(∠DCE)=ED/CD (по
определению)
sin60°=ED/CD (sin60°=√3/2 по
таблице)
√3/2=ED/40
ED=40√3/2
sin(∠ABF)=AF/AB (по
определению)
sin45°=ED/AB
AB=ED/sin45° (sin45°=√2/2 по
таблице)
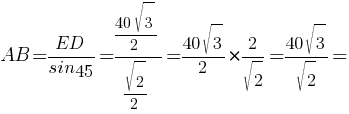
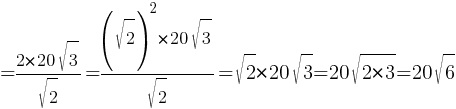
Ответ: 20√6
Поделитесь решением
Присоединяйтесь к нам...
Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
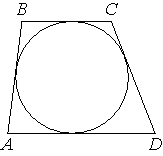Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
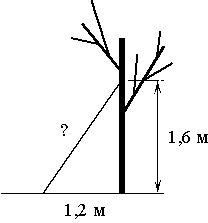Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-01-22 19:06:55) адэлина: начерчите углы АВС-120 И ДВС-45 с общей стороны ВСтак, чтобы они лежали по одну сторону от нее