Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=6, AD=13, AC=38. Найдите AO.
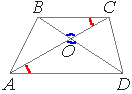Рассмотрим треугольники AOD и BOC.
По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда:
∠DAO=∠BCO (накрест лежащие углы).
∠AOD=∠BOC (вертикальные углы).
Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Следовательно, можем записать пропорцию:
AD/BC=AO/OC
13/6=AO/OC
13*OC=6*AO
При этом AO+OC=AC=38
OC=38-AO, подставляем это равенство в ранее полученную пропорцию:
13*(38-AO)=6*AO
494-13*AO=6*AO
494=6*AO+13*AO
494=19*AO
AO=494/19=26
Ответ: 26
Поделитесь решением
Присоединяйтесь к нам...
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, AC=64. Найдите AK.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудалённая от концов отрезка.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-04-14 12:43:44) Администратор: Евгения: 6*AO+13*AO=19AO
(2019-04-14 12:01:32) Евгения: откуда взялось 19