
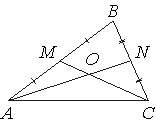
 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Отрезки AN и CM - являются
медианами треугольника ABC.
Тогда, применяя первое свойство медианы, можем записать:
CO/OM=2/1, т.е. CO=2OM
При этом CM=CO+OM
15=CO+OM, подставляем в это уравнение первое равенство:
15=2OM+OM
15=3OM
OM=5
Ответ: 5
Поделитесь решением
Присоединяйтесь к нам...
 Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
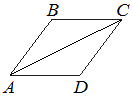 В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
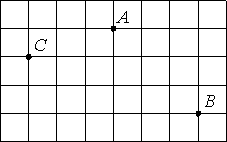 На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
 Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Комментарии: