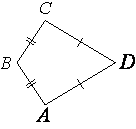В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
Проведем отрезок BD.
Рассмотрим треугольники BCD и BAD:
AB=BC (по условию)
AD=CD (по условию)
BD - общая сторона
По
третьему признаку (по трем сторонам) данные треугольники равны.
Следовательно, ∠С=∠A, обозначим как "х".
По теореме о сумме углов n-угольника получаем уравнение (n в нашем услучае равен 4):
180°(n-2)=∠A+∠B+∠C+∠D
180°(4-2)=x+133°+x+173°
180°*2=2x+306°
360°-306°=2x
x=27°
Ответ: 27
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
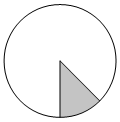Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
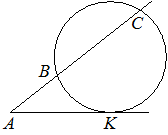Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, BC=32. Найдите AK.
Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-14 18:55:22) Администратор: Людмила, можно, но лучше показать по какой формуле.
(2017-05-13 18:47:10) Людмила: Можно сразу использовать утверждение, что сумма углов четырехугольника равна 360 град.