В трапеции ABCD известно, что AD=4, BC=3, а её площадь равна 84. Найдите площадь трапеции BCNM, где MN — средняя линия трапеции ABCD.
Площадь трапеции вычисляется по формуле: произведение полусуммы оснований и высоты.
Т.е. для трапеции ABCD можем записать:
SABCD=h*(AD+BC)/2
84=h*(4+3)/2
168=7h
h=24
Для трапеции BCNM:
SBCNM=hBCNM*(MN+BC)/2
MN - это средняя линия, значит длина равна полусумме оснований:
MN=(AD+BC)/2=(4+3)/2=3,5
Высота трапеции BCNM равна половине высоты трапеции ABCD (по
теореме Фалеса), тогда:
SBCNM=hBCNM*(MN+BC)/2=(h/2)*(3,5+BC)/2=(24/2)*(3,5+3)/2=12*3,25=39
Ответ: 39
Поделитесь решением
Присоединяйтесь к нам...
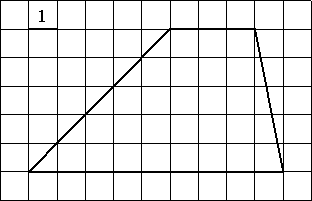Найдите площадь трапеции, изображённой на рисунке.
В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
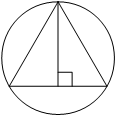Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
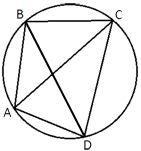Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
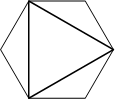Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: