
 Радиус окружности с центром в точке O равен 29, длина хорды AB равна 40 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Радиус окружности с центром в точке O равен 29, длина хорды AB равна 40 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
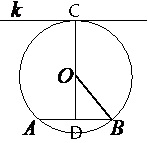 Проведем отрезок OB как показано на рисунке.
Проведем отрезок OB как показано на рисунке.
Расстояние от
хорды AB до параллельной ей
касательной k обозначено как CD.
CD=OC+OD, OC - это радиус окружности, найдем OD.
По условию задачи k||AB. CD перпендикулярен k (по
свойству касательной), тогда CD перпендикулярен и AB (т.к. CD - секущая для параллельных прямых, и внутренние
накрест-лежащие углы равны), значит треугольник OBD
прямоугольный.
DB=AB/2=40/2=20 (по
второму свойству хорды)
OB равен радиусу окружности.
Тогда по
теореме Пифагора:
OB2=OD2+DB2
292=OD2+202
841=OD2+400
OD2=841-400=441
OD=21
CD=OC+OD=29+21=50
Ответ: 50
Поделитесь решением
Присоединяйтесь к нам...
 Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
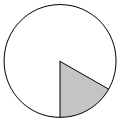 Площадь круга равна 78. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
Площадь круга равна 78. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
 Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
 Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
 Высота AH ромба ABCD делит сторону CD на отрезки DH=21 и CH=8. Найдите высоту ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH=21 и CH=8. Найдите высоту ромба.
Комментарии: