
 Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=28.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=28.
BC||AD (по
определению параллелограмма)
∠BAE=∠EAD (т.к. AE -
биссектриса)
∠EAD=∠BEA (т.к. это
накрест-лежащие углы)
Следовательно, ∠BAE=∠BEA
Получается, что треугольник ABE -
равнобедренный (по
свойству), и AB=BE (по
определению равнобедренного треугольника).
Аналогично с треугольником ECD:
∠CED=∠CDE
EC=CD
Так как AB=CD (по
свойству параллелограмма), то получается, что AB=BE=EC=CD=BC/2=28/2=14.
Ответ: 14
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
 Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
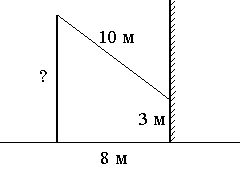 От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
 Площадь прямоугольного треугольника равна 32√
Площадь прямоугольного треугольника равна 32√
Комментарии:
(2015-12-12 17:48:16) Администратор: Галина, Вы совершенно правы, спасибо, что заметили. Исправлено.
(2015-12-11 08:00:19) Галина: У Вас допущена ошибка: АВ=ВЕ=ЕС=СД, значит АВ=1/2 ВС=1/2 от 28=14 Ответ 14