
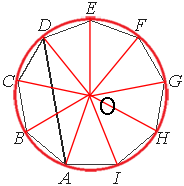
 ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
 Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Очевидно, что отрезки, проведенные из центра окружности к углам девятиугольника образуют равные углы, так как разбивают девятиугольник на равные треугольники.
Такой угол (например ∠DOE) равен 360°/9=40°
Тогда ∠AOC, который опирается на дугу ABC равен:
∠AOC=40°*2=80°
∠AOC является
центральным, следовательно градусная мера дуги ABC тоже равна 80°
∠ADC тоже опирается на эту же дугу, но является
вписанным, следовательно:
∠ADC=80°/2=40° (по
теореме о вписанном угле)
Ответ: 40
Поделитесь решением
Присоединяйтесь к нам...
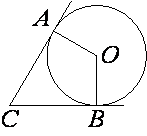 В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
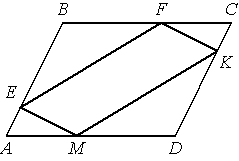 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
 Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Комментарии: