Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
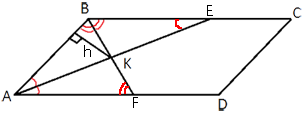Обозначим точки пересечения
биссектрис со сторонами как показано на рисунке.
∠FAK=∠BEK (т.к. это
накрест-лежащие углы).
Получается, что ∠BAK=∠BEK, следовательно треугольник ABE -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда AB=BE.
Треугольники ABK и EBK равны по
первому признаку равенства треугольников.
Следовательно и
высоты у этих треугольников тоже равны.
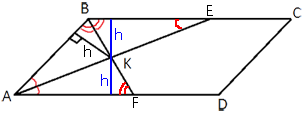Аналогично, равны и треугольники ABK и AFK.
Получается, что высота
параллелограмма равна 2h.
Площадь
параллелограмма равна SABCD=2h*BC=2*7*19=266
Ответ: 266
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, BC=6, sinA=0,6. Найдите AB.
Найдите площадь параллелограмма, изображённого на рисунке.
ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
ABCDEFGHI – правильный девятиугольник. Найдите угол BAG. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Треугольник со сторонами 1, 2, 4 не существует.
3) Сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-29 00:01:54) Администратор: Нина, к сожалению, у меня нет такой информации.
(2017-05-24 03:23:20) нина: задача из какой части
(2015-05-06 22:00:08) Алексей : Спасибо огромное, понятное дело вы думаете что задачи легкие, но для нашей не полностью сложившейся головы они трудные. Так что спс браток, ваще выручил. Молодчик.