
 Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
Каждая ступенька представляет из себя
прямоугольный треугольник, следовательно расстояние между точками А и В будет равняться сумме гипотенуз ступеней.
По
теореме Пифагора:
Квадрат гипотенузы ступени равен 10,52+362=110,25+1296=1406,25
Тогда длина гипотенузы равна √
Т.к. ступеней 20 шт., то расстояние от А до В составляет 20*37,5=750 см, что равняется 7,5 м.
Ответ: 7,5
Поделитесь решением
Присоединяйтесь к нам...
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
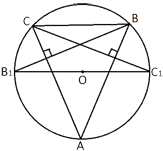 Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
 Медиана равностороннего треугольника равна 9√
Медиана равностороннего треугольника равна 9√
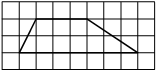 На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Комментарии: