
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ71 –Η–Ζ 1087 |
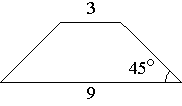 –£ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―Ä–Α–≤–Ϋ―΄ 3 –Η 9, –Α –Ψ–¥–Η–Ϋ –Η–Ζ ―É–≥–Μ–Ψ–≤ –Φ–Β–Ε–¥―É –±–Ψ–Κ–Ψ–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι –Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ ―Ä–Α–≤–Β–Ϋ 45¬Α. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η.
–£ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―Ä–Α–≤–Ϋ―΄ 3 –Η 9, –Α –Ψ–¥–Η–Ϋ –Η–Ζ ―É–≥–Μ–Ψ–≤ –Φ–Β–Ε–¥―É –±–Ψ–Κ–Ψ–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι –Η –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ ―Ä–Α–≤–Β–Ϋ 45¬Α. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η.
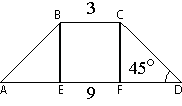 –ü―Ä–Ψ–≤–Β–¥–Β–Φ –≤―΄―¹–Ψ―²―΄ –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β. –‰ ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ CDF. –≠―²–Ψ
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ (―².–Κ. /CFD - –Ω―Ä―è–Φ–Ψ–Ι).
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –≤―΄―¹–Ψ―²―΄ –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β. –‰ ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ CDF. –≠―²–Ψ
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ (―².–Κ. /CFD - –Ω―Ä―è–Φ–Ψ–Ι).
–ü–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –Ψ ―¹―É–Φ–Φ–Β ―É–≥–Μ–Ψ–≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –Ϋ–Α–Ι–¥–Β–Φ ―É–≥–Ψ–Μ FCD
/FCD=180¬Α-90¬Α-45¬Α=45¬Α. –½–Α–Φ–Β―²–Η–Φ, ―΅―²–Ψ /FCD=/FDC. –Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ
―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ―΄–Ι (–Ω–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α). –û―²―¹―é–¥–Α ―¹–Μ–Β–¥―É–Β―², ―΅―²–Ψ FD=FC (–Ω–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α).
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABE. /BAE=/FDC=45¬Α (―².–Κ. –Ω–Ψ ―É―¹–Μ–Ψ–≤–Η―é –Ζ–Α–¥–Α―΅–Η
―²―Ä–Α–Ω–Β―Ü–Η―è ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Α―è).
–ê–Ϋ–Α–Μ–Ψ–≥–Η―΅–Ϋ–Ψ –Ω–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –Ψ ―¹―É–Φ–Φ–Β ―É–≥–Μ–Ψ–≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –Ω–Ψ–Μ―É―΅–Η–Φ, ―΅―²–Ψ /ABE=180¬Α-90¬Α-45¬Α=45¬Α, –Α ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ (–Α–Ϋ–Α–Μ–Ψ–≥–Η―΅–Ϋ–Ψ –Ω―Ä–Β–¥―΄–¥―É―â–Β–Φ―É ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ―É) ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABE -
―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ―΄–Ι.
–ü―Ä–Η―΅–Β–Φ ―ç―²–Η ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η ―Ä–Α–≤–Ϋ―΄ (AB=CD, BE=CF –Η /ABE=/FCD -
–Ω–Β―Ä–≤―΄–Ι –Ω―Ä–Η–Ζ–Ϋ–Α–Κ ―Ä–Α–≤–Β–Ϋ―¹―²–≤–Α)=> AE=FD.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―΅–Β―²―΄―Ä–Β―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ BCFE.
–Δ.–Κ. BC||EF, BE –Η FC - –≤―΄―¹–Ψ―²―΄, ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ /BEF=90¬Α=/CFE. /EBC=/BCF=90¬Α. –Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ ―΅–Β―²―΄―Ä–Β―Ö―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ BCFE -
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ => BC=EF.
–Δ–Β–Ω–Β―Ä―¨ –Φ–Ψ–Ε–Β–Φ –Ζ–Α–Ω–Η―¹–Α―²―¨:
AD=AE+EF+FD, 9=AE+3+FD, 9=AE+3+AE
6=2*AE => AE=3.
–Δ.–Κ. AE=BE=3, –Α BE-–≤―΄―¹–Ψ―²–Α ―²―Ä–Α–Ω–Β―Ü–Η–Η, ―²–Ψ ―²–Β–Ω–Β―Ä―¨ –Φ–Ψ–Ε–Β–Φ –≤―΄―΅–Η―¹–Μ–Η―²―¨
–Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η.
S―²―Ä–Α–Ω–Β―Ü–Η–Η=(BC+AD)/2*BE
S―²―Ä–Α–Ω–Β―Ü–Η–Η=(3+9)/2*3=18.
–û―²–≤–Β―²: S―²―Ä–Α–Ω–Β―Ü–Η–Η=18.
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –ü―Ä―è–Φ–Α―è, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Β AC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η BC –≤ ―²–Ψ―΅–Κ–Α―Ö M –Η N ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ, AB=28, AC=24, MN=18. –ù–Α–Ι–¥–Η―²–Β AM.
–ü―Ä―è–Φ–Α―è, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α―è ―¹―²–Ψ―Ä–Ψ–Ϋ–Β AC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η BC –≤ ―²–Ψ―΅–Κ–Α―Ö M –Η N ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ, AB=28, AC=24, MN=18. –ù–Α–Ι–¥–Η―²–Β AM.
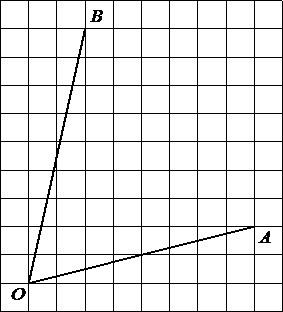 –ù–Α–Ι–¥–Η―²–Β ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α
AOB.
–ù–Α–Ι–¥–Η―²–Β ―²–Α–Ϋ–≥–Β–Ϋ―¹ ―É–≥–Μ–Α
AOB.
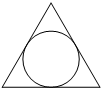 –Γ―²–Ψ―Ä–Ψ–Ϋ–Α ―Ä–Α–≤–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Β–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 18√3. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ ―ç―²–Ψ―² ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
–Γ―²–Ψ―Ä–Ψ–Ϋ–Α ―Ä–Α–≤–Ϋ–Ψ―¹―²–Ψ―Ä–Ψ–Ϋ–Ϋ–Β–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α 18√3. –ù–Α–Ι–¥–Η―²–Β ―Ä–Α–¥–Η―É―¹ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ ―ç―²–Ψ―² ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
 –Θ–≥–Μ―΄ –Ω―Ä–Η –Ψ–¥–Ϋ–Ψ–Φ –Η–Ζ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ―΄ 48¬Α –Η 42¬Α, –Α –Ψ―²―Ä–Β–Ζ–Κ–Η, ―¹–Ψ–Β–¥–Η–Ϋ―è―é―â–Η–Β ―¹–Β―Ä–Β–¥–Η–Ϋ―΄ –Ω―Ä–Ψ―²–Η–≤–Ψ–Ω–Ψ–Μ–Ψ–Ε–Ϋ―΄―Ö ―¹―²–Ψ―Ä–Ψ–Ϋ ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ―΄ 6 –Η 3. –ù–Α–Ι–¥–Η―²–Β –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―²―Ä–Α–Ω–Β―Ü–Η–Η.
–Θ–≥–Μ―΄ –Ω―Ä–Η –Ψ–¥–Ϋ–Ψ–Φ –Η–Ζ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ―΄ 48¬Α –Η 42¬Α, –Α –Ψ―²―Ä–Β–Ζ–Κ–Η, ―¹–Ψ–Β–¥–Η–Ϋ―è―é―â–Η–Β ―¹–Β―Ä–Β–¥–Η–Ϋ―΄ –Ω―Ä–Ψ―²–Η–≤–Ψ–Ω–Ψ–Μ–Ψ–Ε–Ϋ―΄―Ö ―¹―²–Ψ―Ä–Ψ–Ϋ ―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ―΄ 6 –Η 3. –ù–Α–Ι–¥–Η―²–Β –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η―è ―²―Ä–Α–Ω–Β―Ü–Η–Η.
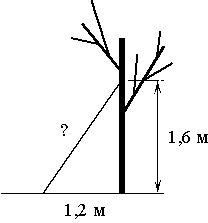 –ö–Α–Κ–Ψ–≤–Α –¥–Μ–Η–Ϋ–Α (–≤ –Φ–Β―²―Ä–Α―Ö) –Μ–Β―¹―²–Ϋ–Η―Ü―΄, –Κ–Ψ―²–Ψ―Ä―É―é –Ω―Ä–Η―¹–Μ–Ψ–Ϋ–Η–Μ–Η –Κ –¥–Β―Ä–Β–≤―É, –Β―¹–Μ–Η –≤–Β―Ä―Ö–Ϋ–Η–Ι –Β―ë –Κ–Ψ–Ϋ–Β―Ü –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –Ϋ–Α –≤―΄―¹–Ψ―²–Β 1,6 –Φ –Ϋ–Α–¥ –Ζ–Β–Φ–Μ―ë–Ι, –Α –Ϋ–Η–Ε–Ϋ–Η–Ι –Ψ―²―¹―²–Ψ–Η―² –Ψ―² ―¹―²–≤–Ψ–Μ–Α –¥–Β―Ä–Β–≤–Α –Ϋ–Α 1,2 –Φ?
–ö–Α–Κ–Ψ–≤–Α –¥–Μ–Η–Ϋ–Α (–≤ –Φ–Β―²―Ä–Α―Ö) –Μ–Β―¹―²–Ϋ–Η―Ü―΄, –Κ–Ψ―²–Ψ―Ä―É―é –Ω―Ä–Η―¹–Μ–Ψ–Ϋ–Η–Μ–Η –Κ –¥–Β―Ä–Β–≤―É, –Β―¹–Μ–Η –≤–Β―Ä―Ö–Ϋ–Η–Ι –Β―ë –Κ–Ψ–Ϋ–Β―Ü –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –Ϋ–Α –≤―΄―¹–Ψ―²–Β 1,6 –Φ –Ϋ–Α–¥ –Ζ–Β–Φ–Μ―ë–Ι, –Α –Ϋ–Η–Ε–Ϋ–Η–Ι –Ψ―²―¹―²–Ψ–Η―² –Ψ―² ―¹―²–≤–Ψ–Μ–Α –¥–Β―Ä–Β–≤–Α –Ϋ–Α 1,2 –Φ?
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2015-05-25 15:16:38) –Δ–Α–Ϋ―è: –Γ–Ω–Α―¹–Η–±–Ψ, ―ç―²–Ψ―² ―¹–Α–Ι―² –Ψ―΅–Β–Ϋ―¨ –Ω–Ψ–Φ–Ψ–≥–Α–Β―²!