
 В параллелограмме ABCD точка E — середина стороны CD. Известно, что EA=EB. Докажите, что данный параллелограмм — прямоугольник.
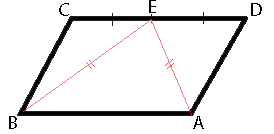
В параллелограмме ABCD точка E — середина стороны CD. Известно, что EA=EB. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники BCE и EDA. CE=ED, т.к. точка E - середина CD, EA=EB (из условия задачи), CB=AD (по свойству параллелограмма). Соответственно, треугольники BCE и EDA равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что /BCE=/EDA.
BC||AD (по определению параллелограмма), рассмотрим сторону CD как секущую к этим параллельным сторонам. Тогда получается, что сумма углов BCE и EDA равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.
Теперь рассмотрим стороны AB и CD, они параллельны (тоже по определению параллелограмма). Рассмотрим сторону BC как секущую к этим параллельным сторонам.
/CBA и /ECB - внутренние односторонние. Следовательно их сумма равна 180°. А так как /ECB=90°, то /CBA тоже равен 90°.
Аналогично доказывается, что /DAB тоже равен 90°.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
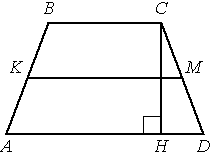 В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
 Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Какие из данных утверждений верны? Запишите их номера.
1) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
2) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
3) У равнобедренного треугольника есть центр симметрии.
 Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Комментарии: