
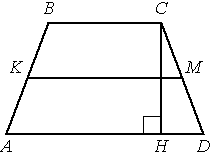
 В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
Средняя линия трапеции Lср=(AD+BC)/2, отсюда AD=2*Lср-BC.
Проведем еще одну высоту из вершины B
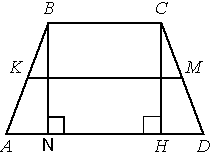 и рассмотрим треугольники CDH и ABN. AB=CD (по условию задачи), BN=CH, т.к. BCHN -
прямоугольник, образованный параллельными сторонами трапеции и перпендикулярами к ним. Следовательно, применив
теорему Пифагора, получим, что HD=NA
и рассмотрим треугольники CDH и ABN. AB=CD (по условию задачи), BN=CH, т.к. BCHN -
прямоугольник, образованный параллельными сторонами трапеции и перпендикулярами к ним. Следовательно, применив
теорему Пифагора, получим, что HD=NA
AD=AN+NH+HD, AD=2*HD+NH, NH=BC (т.к. BCHN - прямоугольник), тогда AD=2*HD+BC,
HD=(AD-BC)/2
Ранее мы выяснили, что AD=2*Lср-BC=2*16-4=28, тогда HD=(28-4)/2=12.
Ответ: HD=12.
Поделитесь решением
Присоединяйтесь к нам...
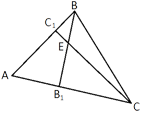 Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
 Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
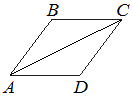 В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
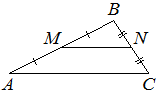 Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.
 В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
Комментарии: