
 Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
 Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту трапеции.
Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту трапеции.
Проведем высоту как показано на рисунке. Получившийся треугольник является
прямоугольным. По
определению синуса можем записать: sin30°=h/5 => h=5*sin30°, sin30°=1/2 (
табличное значение).
h=5*1/2=2,5.
Sтрапеции=(3+9)/2*2,5=15
Ответ: площадь трапеции равна 15.
Поделитесь решением
Присоединяйтесь к нам...
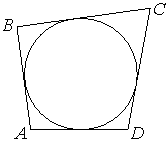 Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
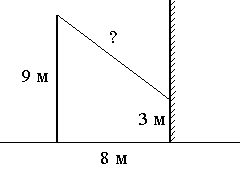 От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
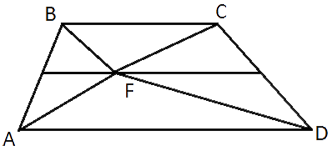 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
 В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Комментарии: