Точка О – центр окружности, /AOB=72° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию /AOB=72°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 72°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 72/2=36.
Ответ: /ACB=36°.
Поделитесь решением
Присоединяйтесь к нам...
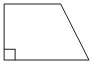Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
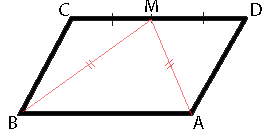В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA=MB. Докажите, что данный параллелограмм — прямоугольник.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
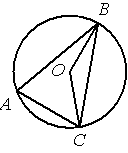Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: