
 Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
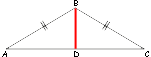 Проведем высоту BD.
Проведем высоту BD.
По
свойству
равнобедренного треугольника:
высота, проведенная к основанию так же является и
медианой.
Следовательно, AD=DC=AC/2=48/2=24
Чтобы вычислить эту высоту треугольника воспользуемся
теоремой Пифагора:
AB2=BD2+AD2
252=BD2+242
625=BD2+576
BD2=49
BD=7
Площадь треугольника: S=ah/2=AC*BD/2
S=48*7/2=168
Ответ: S=168
Поделитесь решением
Присоединяйтесь к нам...
 Катеты прямоугольного треугольника равны 5√
Катеты прямоугольного треугольника равны 5√
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
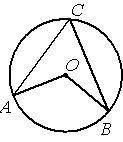 Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
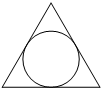 Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
Комментарии: