Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 40:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
Пусть AD -
биссектриса, описанная в условии.
BC - сторона, равная 30.
Рассмотрим треугольник ADC.
Для этого треугольника CO -
биссектриса,
По
свойству биссектрисы:
AO/OD=AC/CD=40/1
AC=40*CD
Рассмотрим треугольник ABD.
Для этого треугольника BO -
биссектриса,
По
свойству биссектрисы:
AO/OD=AB/BD=40/1
AB=40*BD
Складываем полученные равенства:
AC+AB=40*CD+40*BD
AC+AB=40(CD+BD), CD+BD=BC=30
AC+AB=40*30
AC+AB=1200
PABC=AC+AB+BC=1200+30=1230
Ответ: PABC=1230
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам.
2) Не существует прямоугольника, диагонали которого взаимно перпендикулярны.
3) В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.
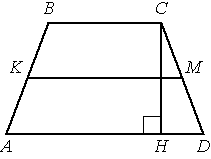В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
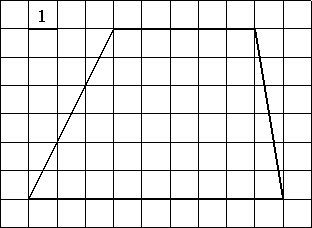Найдите площадь трапеции, изображённой на рисунке.
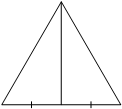Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2020-03-31 20:27:05) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2020-03-12 21:48:56) : . В треугольнике ABC проведена биссектриса CK. Найдите периметр треугольника ABC, если BC = 8, BK = 3, .