
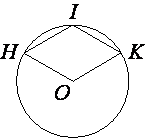 Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OKI. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OKI. Ответ дайте в градусах.
HO=KO (т.к. это радиусы окружности)
HO=KO=HI=IK (по
определению ромба)
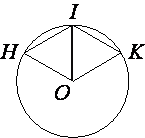 Проведем отрезок OI.
Проведем отрезок OI.
OI тоже радиус окружности, следовательно HO=KO=HI=IK=OI
Следовательно, треугольники HIO и KIO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
Следовательно, /OKI=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
Стороны AC, AB, BC треугольника ABC равны 2√
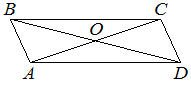 Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
 В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
 Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
Комментарии: