
 В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
По
теореме о сумме углов треугольника: 180°=/A+/B+/C, отсюда /B=180°-/A-/C=180°-20°-50°=110°.
/ABD=/B/2=55° (т.к. BD -
биссектриса).
Рассмотрим треугольник BHC, по
теореме о сумме углов треугольника получаем 180°=50°+90°+/CBH => /CBH=40°.
Тогда искомый угол /DBH=/B-/ABD-/CBH=110°-55°-40°=15°.
Ответ: /DBH=15°
Поделитесь решением
Присоединяйтесь к нам...
 Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
 Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина – 28 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина – 28 см. Найдите расстояние между точками A и B (в метрах).
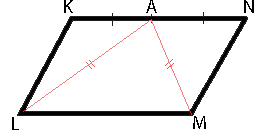 В параллелограмме KLMN точка A — середина стороны KN. Известно, что AL=AM. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка A — середина стороны KN. Известно, что AL=AM. Докажите, что данный параллелограмм — прямоугольник.
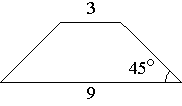 В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
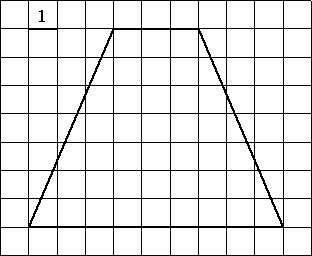 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Комментарии: