
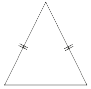
 Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
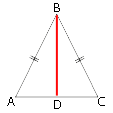 Проведем высоту BD.
Проведем высоту BD.
По
свойству
равнобедренного треугольника:
высота, проведенная к основанию так же является и
медианой.
Следовательно, AD=DC=AC/2=30/2=15
Чтобы вычислить эту высоту треугольника воспользуемся
теоремой Пифагора:
AB2=BD2+AD2
252=BD2+152
625=BD2+225
BD2=400
BD=20
Площадь треугольника: S=ah/2=AC*BD/2
S=30*20/2=300
Ответ: S=300
Поделитесь решением
Присоединяйтесь к нам...
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
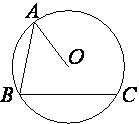 Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=43° и ∠OAB=13°. Найдите угол BCO. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=43° и ∠OAB=13°. Найдите угол BCO. Ответ дайте в градусах.
 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
 Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
Комментарии: