
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 4, тангенс угла BAC равен 0,75. Найдите радиус вписанной окружности треугольника ABC.
 Рассмотрим треугольник АРС.
Рассмотрим треугольник АРС.
По определению tgBAC=СР/АР=0,75 => CP=0,75AP
Радиус вписанной в прямоугольный треугольник окружности равен r=(AP+CP-AC)/2
Подставляем СР=0,75AP
2r=AP+0,75AP-AC
2r=1,75AP-AC
2*4+AC=1,75AP
AP=(8+AC)/1,75 (поставим здесь пометку 1, чуть позднее вернемся к ней)
По
теореме Пифагора AC2=AP2+CP2
AC2=AP2+(0,75AP)2
AC2=AP2(1+0,752)
AC2=AP2*(1+0,5625)
AC2=AP2*1,5625
AC=AP*1,25
Из пометки 1 подставляем AP
AC=1,25*(8+AC)/1,75
1,75AC=1,25(8+AC) сократим на 25
0,07AC=0,05(8+AC) умножим правую и левую часть уравнения на 100 (для удобства)
7AC=5(8+AC)
7AC=40+5AC
2AC=40
AC=20
Теперь рассмотрим большой треугольник АВС и проведем для него те же операции, но сразу с числами
tgBAC=BC/AC => 0,75=BC/20 => BC=0,75*20=15
По
теореме Пифагора запишем AB2=AC2+BC2
AB2=202+152
AB2=400+225=625
AB=25
Теперь все полученые данные подставляем в формулу радиуса окружности
R=(AC+BC-AB)/2
R=(20+15-25)/2
R=10/2
R=5
Ответ: R=5.
Поделитесь решением
Присоединяйтесь к нам...
Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме её оснований.
2) Диагонали ромба перпендикулярны.
3) Площадь треугольника меньше произведения двух его сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
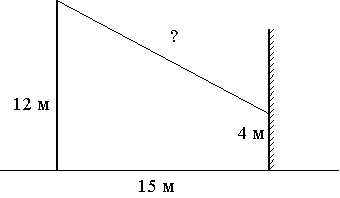 От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.
От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.
Синус острого угла A треугольника ABC равен  . Найдите CosA.
. Найдите CosA.
 В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
 ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
Комментарии:
(2017-03-17 01:56:14) Администратор: Евгения, есть соответствующая теорема.
(2017-03-16 10:50:32) Евгения: откуда берется это утверждение: \"Радиус вписанной в прямоугольный треугольник окружности равен r=(AP+CP-AC)/2\" ?
(2015-09-19 19:08:54) Людмила: Огромное спасибо за помощь и удобный интерфейс сайта!
(2015-02-25 14:35:41) мария: спасибо за ваш сайт