
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
Рассмотрим треугольник BDH.
Данный треугольник
прямоугольный, следовательно можно применить
теорему Пифагора:
BD2=HD2+BH2
652=632+BH2
4225=3969+BH2
BH2=256
BH=16
Найдем площадь
параллелограмма:
S=AD*BH=(AH+HD)*BH=(1+63)*16=1024
Ответ: 1024
Поделитесь решением
Присоединяйтесь к нам...
 Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
 Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
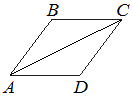 В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
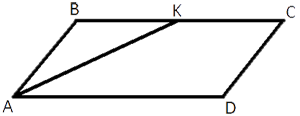 Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
Комментарии:
(2017-02-20 20:22:44) Администратор: Сумая, в чем вопрос.
(2017-02-20 18:12:06) Сумая: Сумма треугольников