
 Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=54. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=54. Найдите площадь ромба.
Площадь
ромба равна S=ah, где a - сторона ромба, h - высота ромба.
AD=AH+HD=21+54=75.
AD=AB=BC=CD (по
определению ромба).
Рассмотрим треугольник ABH.
ABH -
прямоугольный (т.к. BH -
высота), тогда по
теореме Пифагора:
AB2=BH2+AH2
752=BH2+212
5625=BH2+441
BH2=5184
BH=72
Sромба=AD*BH=75*72=5400
Ответ: Sромба=5400
Поделитесь решением
Присоединяйтесь к нам...
 Из вершины прямого угла C треугольника
ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
Из вершины прямого угла C треугольника
ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 11°?
 В треугольнике ABC угол C равен 90°, BC=5, AC=2.
В треугольнике ABC угол C равен 90°, BC=5, AC=2.
Найдите tgB.
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 154°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 154°. Найдите угол C. Ответ дайте в градусах.
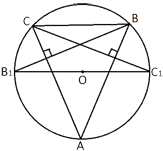 Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Комментарии: