Лестница соединяет точки A и B. Высота каждой ступени равна 10,5 см, а длина – 36 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, на которую поднимается лестница (в метрах).
Чтобы определить высоту, на которую поднимается лестница, надо узнать количество ступеней и умножить на высоту ступени.
Каждая ступенька представляет из себя
прямоугольный треугольник, следовательно расстояние между точками А и В будет равняться сумме гипотенуз ступеней.
По
теореме Пифагора:
Квадрат гипотенузы одной ступени равен 10,52+362=110,25+1296=1406,25
Тогда длина гипотенузы равна √
1500/37,5=40 ступеней составляют лестницу.
10,5*40=420 см - высота лестницы = 4,2 м
Ответ: 4,2
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=15, AC=25, NC=22.
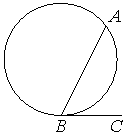На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-02-24 20:04:10) Администратор: Марина, потому, что \"каждая ступенька - это прямоугольный треугольник\", а расстояние между точками - это гипотенуза этого треугольника. Можно, конечно, решать и без теоремы Пифагора, через теорему косинусов, или через радиус описанной окружности, но это усложнит решение.
(2017-02-24 19:04:43) Марина: Почему решается по теореме пифагора?