Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Рассмотрим каждое утверждение:
1) "Существует квадрат, который не является прямоугольником" - это утверждение неверно, т.к. противоречит определению квадрата.
2) "Если два угла треугольника равны, то равны и противолежащие им стороны", это утверждение верно по
свойству равнобедренного треугольника.
3) "Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.", это утверждение верно по
свойству углов.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
Точка О – центр окружности, /ACB=25° (см. рисунок). Найдите величину угла AOB (в градусах).
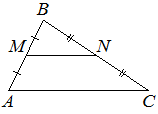Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CMD.
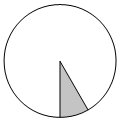Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: