
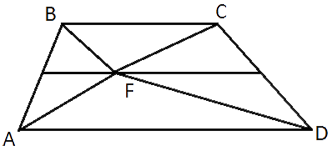 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
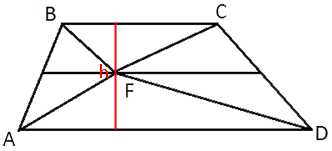 Проведем через точку F
высоту
трапеции h.
Проведем через точку F
высоту
трапеции h.
Высота h делится точкой F пополам, т.к. располагается на
средней линии, а средняя линия делит стороны трапеции пополам.
Таким образом получается, что высота обоих треугольников равна h/2.
Площадь треугольника равна половине произведения высоты на основание треугольника.
Площадь трапеции равна произведению полусуммы оснований на высоту.
SBFC=(h/2)*BC/2
SAFD=(h/2)*AD/2
SBFC+SAFD=(h/2)*BC/2+(h/2)*AD/2=(h/2)(BC+AD)/2=(h*(BC+AD)/2)/2=SABCD/2
Поделитесь решением
Присоединяйтесь к нам...
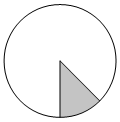 Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
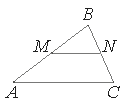 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=28. Площадь треугольника ABC равна 162. Найдите площадь треугольника MBN.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=28. Площадь треугольника ABC равна 162. Найдите площадь треугольника MBN.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
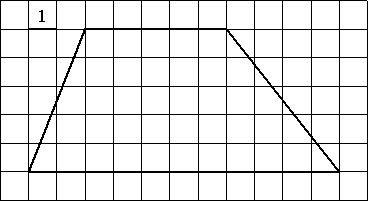 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 28. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 28. Найдите стороны треугольника ABC.
Комментарии: