
 Площадь параллелограмма ABCD равна 5. Точка E – середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 5. Точка E – середина стороны AD. Найдите площадь трапеции AECB.
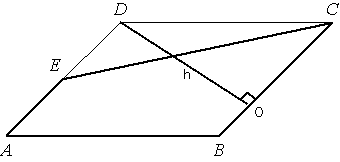 Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Sпараллелограмма=BC*h=5
А площадь
трапеции равна произведению полусуммы оснований на высоту.
Sтрапеции=h*(BC+AE)/2.
AE=AD/2 (по условию задачи).
AD=BC (по
свойству параллелограмма).
Следовательно AE=BC/2.
Тогда Sтрапеции=h*(BC+BC/2)/2 = h*(3*BC/2)/2 = h*3*BC/4=h*BC*3/4 = Sпарал-ма*3/4=5*3/4=3,75.
Ответ: Sтрапеции=3,75.
Поделитесь решением
Присоединяйтесь к нам...
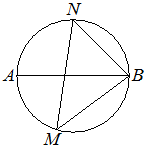 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
 Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
 Лестница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
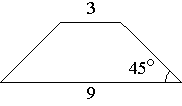 В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Комментарии:
(2015-05-25 21:18:55) Администратор: BC+BC/2=(2BC)/2+BC/2=(3BC)/2
(2015-05-25 19:09:28) : а откуда вы взял 3 в S трапеции
(2015-05-25 19:09:05) : 543