
 В трапеции ABCD AB=CD, ∠BDA=67° и ∠BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=67° и ∠BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
∠ADC=∠BDA+∠BDC=67°+28°=95°
Т.к. AB=CD, то
трапеция ABCD -
равнобедренная.
Тогда ∠ADC=∠BAD=95° (по
свойству равнобедренной трапеции).
Рассмотрим треугольник ABD:
По
теореме о сумме углов треугольника:
180°=∠BAD+∠ADB+∠ABD
180°=95°+67°+∠ABD
∠ABD=18°
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
 Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
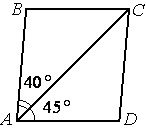 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол параллелограмма.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BKC.
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC.
Комментарии: