
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C . Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C . Ответ дайте в градусах.
∠CBA - является
смежным внешнему углу, следовательно, 180°=∠CBA+146°
∠CBA=180°-146°=34°
Так как AC=BC, то треугольник ABC -
равнобедренный.
Значит ∠CBA=∠CAB=34° (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠CBA+∠CAB+∠C
180°=34°+34°+∠C
∠C=180°-34°-34°
∠C=112°
Ответ: 112
Поделитесь решением
Присоединяйтесь к нам...
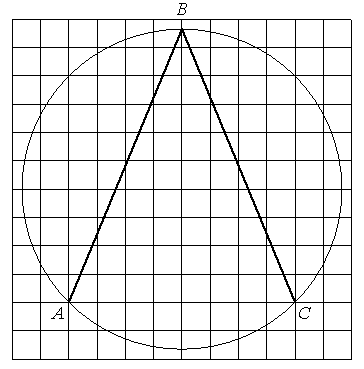 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
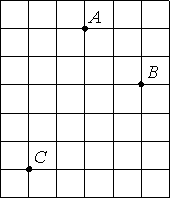 На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
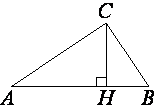 В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
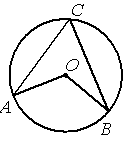 Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=40.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=40.
Комментарии:
(2017-12-17 21:44:06) Администратор: про, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-12-13 19:58:01) про: найдите наибольший угол остроугольного равнобедренноготреугольника один из углов которого равен 20 градусовюответ дайте градусах
(2017-02-23 14:26:17) Качёк: Щас бы в 9-ом классе не уметь считать xD
(2015-05-11 20:33:08) Администратор: Дима, я добавил строку в решение, чтобы стало понятней, но вообще-то в 9-ом классе такие уравнения надо уже уметь решать...
(2015-05-11 18:19:32) дима: как получается 112
(2015-04-15 07:20:31) арина: как же хорошо что появился этот сайт