
 Сторона AC треугольника ABC проходит через центр окружности. Найдите
∠C, если ∠A=83°. Ответ дайте в градусах.
Сторона AC треугольника ABC проходит через центр окружности. Найдите
∠C, если ∠A=83°. Ответ дайте в градусах.
Т.к. AC является диаметром, значит треугольник ABC - прямоугольный с гипотенузой AC и ∠B=90° (по
теореме об описанной окружности).
Тогда по теореме сумме углов треугольника:
180°=∠A+∠B+∠C
180°=83°+90°+∠C
∠C=180°-83°-90°
∠C=7°
Ответ: ∠C=7°
Поделитесь решением
Присоединяйтесь к нам...
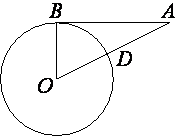 Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
 В треугольнике ABC угол C равен 90°, sinA=0,75, AC=√
В треугольнике ABC угол C равен 90°, sinA=0,75, AC=√
 Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
 Катеты прямоугольного треугольника равны 35 и 120. Найдите высоту, проведённую к гипотенузе.
Катеты прямоугольного треугольника равны 35 и 120. Найдите высоту, проведённую к гипотенузе.
 естница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 19,5 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
естница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 19,5 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
Комментарии:
(2015-05-23 11:18:15) Администратор: Лена, я поправил решение, конечно использовалась не теорема Пифагора, а теорема о сумме углов треугольника.
(2015-05-23 05:42:52) Лена: и 90 ?
(2015-05-23 05:40:42) Лена: откуда 180 градусов?