Сторона AC треугольника ABC проходит через центр окружности. Найдите
∠C, если ∠A=83°. Ответ дайте в градусах.
Т.к. AC является диаметром, значит треугольник ABC - прямоугольный с гипотенузой AC и ∠B=90° (по
теореме об описанной окружности).
Тогда по теореме сумме углов треугольника:
180°=∠A+∠B+∠C
180°=83°+90°+∠C
∠C=180°-83°-90°
∠C=7°
Ответ: ∠C=7°
Поделитесь решением
Присоединяйтесь к нам...
Найдите угол ABC. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.
2) Существует параллелограмм, который не является прямоугольником.
3) Сумма углов тупоугольного треугольника равна 180°.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
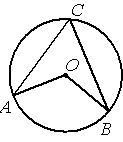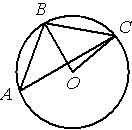Точка О – центр окружности, /AOB=70° (см. рисунок). Найдите величину угла ACB (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-23 11:18:15) Администратор: Лена, я поправил решение, конечно использовалась не теорема Пифагора, а теорема о сумме углов треугольника.
(2015-05-23 05:42:52) Лена: и 90 ?
(2015-05-23 05:40:42) Лена: откуда 180 градусов?