На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=60°. Найдите угол NMB. Ответ дайте в градусах.
Угол NBA является
вписанным для данной окружности. Опирается этот угол на дугу AN. градусная мера дуги AN = /NBA*2=60°*2=120° (по
теореме о вписанном угле).
Градусная мера дуги ANB = 180° (т.к. AB - диаметр), следовательно, градусная мера дуги NB = дуга ANB - дуга AN = 180°-120°=60°
/NMB - тоже является
вписанным в окружность и равен половине градусной меры дуги NB (по
теореме).
/NMB=60°/2=30°
Ответ: /NMB=30°
Поделитесь решением
Присоединяйтесь к нам...
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, описанной около этого треугольника.
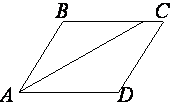Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 14°. Ответ дайте в градусах.
Катеты прямоугольного треугольника равны
√
В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
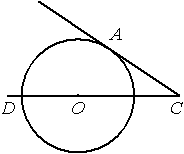Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
140°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: