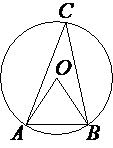Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
∠AOB является
центральным, следовательно, градусная мера дуги, на которую он опирается, равна этому углу.
∠C является
вписанным, следовательно, его градусная мера вдвое меньше, чем градусная мера дуги, на которую он опирается (по
теореме о вписанной угле).
∠C=27°/2=13,5°
Ответ: ∠C=13,5°
Поделитесь решением
Присоединяйтесь к нам...
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.
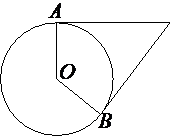Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
В треугольнике ABC угол C прямой, BC=6, cosB=0,3. Найдите AB.
Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: