Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80. Найдите расстояние от хорды AB до параллельной ей касательной k.
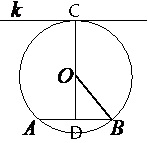Проведем отрезок OB как показано на рисунке.
Расстояние от
хорды AB до параллельной ей
касательной k обозначено как CD.
CD=OC+OD, OC - это радиус окружности, найдем OD.
По условию задачи k||AB. CD перпендикулярен k (по
свойству касательной), тогда CD перпендикулярен и AB (т.к. CD - секущая для параллельных прямых, и внутренние
накрест-лежащие углы равны), значит треугольник OBD
прямоугольный.
DB=AB/2=80/2=40 (по
второму свойству хорды)
OB равен радиусу окружности.
Тогда по
теореме Пифагора:
OB2=OD2+DB2
852=OD2+402
7225=OD2+1600
OD2=7225-1600=5625
OD=75
CD=OC+OD=85+75=160
Ответ: 160
Поделитесь решением
Присоединяйтесь к нам...
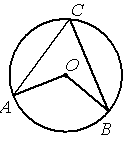Точка О – центр окружности, /AOB=110° (см. рисунок). Найдите величину угла ACB (в градусах).
Площадь прямоугольного треугольника равна 200√
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-03-22 13:31:56) Администратор: Потому, что проведен из центра к точке на окружности, т.е. OB и есть радиус.
(2018-03-16 17:52:17) : Почему ОB равен радиусу окружности?