
Укажите решение неравенства x2-36≤0.
1) (-∞;+∞)
2) (-∞;-6]∪[6;+∞)
3) [-6;6]
4) нет решений
Чтобы решить это неравенство надо найти корни соответствующего уравнения:
x2-36=0
Можно решить это квадратное уравнение через дискриминант, но легче воспользоваться формулой
разность квадратов:
x2-62=0
(x-6)(x+6)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два случая:
1) x-6=0 => x1=6
2) x+6=0 => x2=-6
 Теперь рассмотрим график нашей функции - это парабола.
Теперь рассмотрим график нашей функции - это парабола.
Так как коэффициент при x2 равен 1, т.е. положительный, то ветви параболы направлены вверх.
Нас интересует диапазон, где наша функция меньше или равна нулю (по условию). Это означает, что график функции располагается под осью Х.
В нашем случае, график находится под осью на диапазоне от x1 до x2.
x1 и x2 - это корни, которые мы нашли ранее.
[-6;6]
Ответ: 3)
Поделитесь решением
Присоединяйтесь к нам...
Решите систему уравнений 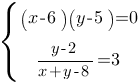
На каком рисунке изображено множество решений системы неравенств
 x+7≤0,5
x+7≤0,5
x+5≤0?
1) 
2) 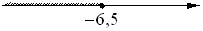
3) 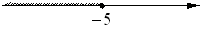
4) 
Поезд, двигаясь равномерно со скоростью 135 км/ч, проезжает мимо столба за 4 секунды. Найдите длину поезда в метрах.
Расходы на одну из статей городского бюджета составляют 1,7%. Выразите эту часть бюджета десятичной дробью.
Поезд, двигаясь равномерно со скоростью 44 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 4 км/ч, за 36 секунд. Найдите длину поезда в метрах.
Комментарии: