Основания трапеции равны 5 и 40, одна из боковых сторон равна 14, а косинус угла между ней и одним из оснований равен 3/5. Найдите площадь трапеции.
Площадь
трапеции равна произведению полусуммы оснований на высоту. Основания нам известны, найдем высоту.
По
определению cos(/CDE)=ED/CD
3/5=ED/14
ED=3*14/5=8,4
По
теореме Пифагора:
CD2=ED2+EC2
142=8,42+EC2
196=70,56+EC2
EC2=125,44
EC=11,2 - это и есть высота
Sтрапеции=EC*(BC+AD)/2
Sтрапеции=11,2*(5+40)/2
Sтрапеции=5,6*45=252
Ответ: Sтрапеции=252
Поделитесь решением
Присоединяйтесь к нам...
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 30 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
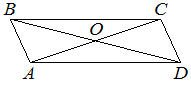Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=24, BD=28, AB=6. Найдите DO.
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, описанной около этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: