Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
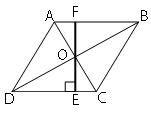Обозначим ключевые точки как показано на рисунке.
Проведем продолжение высоты OE к стороне AB и обозначим точку пересечения как F (как показано на рисунке).
Площадь
ромба (как и
параллелограмма) равна произведению высоты на сторону ромба.
Высота ромба = EF (т.к. EF перпендикулярна CD). Рассмотрим треугольники DOE и BOF.
DO=OB (по второму
свойству ромба)
/DOE=/BOF (т.к. они
вертикальные)
/EDO=/FBO (т.к. это
внутренние накрест-лежащие)
Следовательно, треугольники DOE и BOF равны по
второму признаку.
Тогда OE=OF => EF=2*OE=2*1=2
Sромба=EF*CD=2*9=18
Ответ: Sромба=18
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=84 и BC=BM. Найдите AH.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
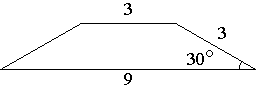Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудалённая от концов отрезка.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: